I wrote a (very long) blog post about those viral math problems and am looking for feedback, especially from people who are not convinced that the problem is ambiguous.
It’s about a 30min read so thank you in advance if you really take the time to read it, but I think it’s worth it if you joined such discussions in the past, but I’m probably biased because I wrote it :)
Hey this is interesting, thanks for sharing!
Honestly, I do disagree that the question is ambiguous. The lack of parenthetical separation is itself a choice that informs order of operations. If the answer was meant to be 9, then the 6/2 would be isolated in parenthesis.
It’s covered in the blog, but this is likely due to a bias towards Strong Juxtaposition rules for parentheses rather than Weak. It’s common for those who learned math into advanced algebra/ beginning Calc and beyond, since that’s the usual method for higher math education. But it isn’t “correct”, it’s one of two standard ways of doing it. The ambiguity in the question is intentional and pervasive.
But it isn’t “correct”
It is correct - it’s The Distributive Law.
it’s one of two standard ways of doing it.
There’s only 1 way - the “other way” was made up by people who don’t remember The Distributive Law and/or Terms (more likely both), and very much goes against the standards.
The ambiguity in the question is
…zero.
My argument is specifically that using no separation shows intent for which way to interpret and should not default to weak juxtaposition.
Choosing not to use (6/2)(1+2) implies to me to use the only other interpretation.
There’s also the difference between 6/2(1+2) and 6/2*(1+2). I think the post has a point for the latter, but not the former.
I originally had the same reasoning but came to the opposite conclusion. Multiplication and division have the same precedence, so I read the operations from left to right unless noted otherwise with parentheses. Thus:
6/2=3
3(1+2)=9
For me to read the whole of 2(1+2) as the denominator in a fraction I would expect it to be isolated in parentheses: 6/(2(1+2)).
Reading the blog post, I understand the ambiguity now, but i’m still fascinated that we had the same criticism (no parentheses implies intent) but had opposite conclusions.
6/2=3
3(1+2)=9
You just did division before brackets, which goes against order of operations rules.
For me to read the whole of 2(1+2) as the denominator in a fraction
You just need to know The Distributive Law and Terms.
Read the linked article
The linked article is wrong. Read this - has, you know, actual Maths textbook references in it, unlike the article.
Hooray! Correct! Anyone who downvoted or disagrees with this needs to read this instead. Includes actual Maths textbooks references.
You lost me on the section when you started going into different calculators, but I read the rest of the post. Well written even if I ultimately disagree!
The reason imo there is ambiguity with these math problems is bad/outdated teaching. The way I was taught pemdas, you always do the left-most operations first, while otherwise still following the ordering.
Doing this for 6÷2(1+2), there is no ambiguity that the answer is 9. You do your parentheses first as always, 6÷2(3), and then since division and multiplication are equal in ordering weight, you do the division first because it’s the left most operation, leaving us 3(3), which is of course 9.
If someone wrote this equation with the intention that the answer is 1, they wrote the equation wrong, simple as that.
There has apparently been historical disagreement over whether 6÷2(3) is equivalent to 6÷2x3
As a logician instead of a mathemetician, the answer is “they’re both wrong because they have proven themselves ambiguous”. Of course, my answer would be RPN to be a jerk or just have more parens to be a programmer
There has apparently been historical disagreement over whether 6÷2(3) is equivalent to 6÷2x3
No, there hasn’t - that’s a false claim by a Youtuber (and others who repeated it) - it is equal to 6÷(2x3) as per The Distributive Law and Terms, and even as per the letter he quoted! Here is where I debunked that claim.
Are you referring to Presh Talwalkar or someone else? How about his reference for historical use, Elizabeth Brown Davis? He also references a Slate article by Tara Haelle. I’ve heard Presh respond to people in the past over questions like this, and I’d love to hear his take on such a debunking. I have a lot of respect for him.
Your “debunk” link seems to debunk a clear rule-change in 1917. I wouldn’t disagree with that. I’ve never heard the variant where there was a clear change in 1917. Instead, it seems there was historical vagueness until the rules we now accept were slowly consolidated. Which actually makes sense.
The Distributive Law obviously applies, but I’m seeing references that would still assert that (6÷2) could at one time have been the portion multiplied with the (3).
And again, from logic I come from a place of avoiding ambiguity. When there is a controversiallly ambiguous form and an undeniablely unambiguous form, the undeniably unambiguous form is preferable.
Yes, the guy who should mind his own business.
How about his reference for historical use
Are you talking about his reference to Lennes’ letter? Lennes’ letter actually completely contradicts his claim that it ever meant anything different.
Elizabeth Brown Davis
Haven’t seen that one. Do you have a link?
He also references a Slate article by
…a journalist. The article ALSO ignores The Distributive Law and Terms.
I wouldn’t disagree with that.
Thank you. And also thank you for being the first person to engage in a proper conversation about it here.
I’ve heard Presh respond to people in the past over questions like this
I’ve seen him respond to people who agree with him. People who tell him he’s wrong he usually ignores. When he DOES respond to them he simply says “The Distributive Property doesn’t apply”. We’re talking about The Distributive LAW, NOT the Distributive Property. It’s called “law” for a reason. i.e. ALWAYS applies. I’ve only ever seen him completely unwilling to engage in any conversation with anyone who points out he’s wrong (contradicting his claim that he “welcomes debate”).
I have a lot of respect for him
Really?? Why’s that? I’m genuinely curious.
I’ve never heard the variant where there was a clear change in 1917
Me either. As far as I can tell it’s just people parroting his misinterpretation of Lennes’ letter.
Instead, it seems there was historical vagueness until the rules we now accept were slowly consolidated
I can’t agree with that. Lennes’ letter shows the same rules in 1917 as we use now. Cajori says the order of operations rules are at least 400 years old, and I have no reason to suspect they changed at all during that time period either. They’re all a natural consequence of the way we have defined the symbols in the first place.
The Distributive Law obviously applies
Again, thank you.
I’m seeing references that would still assert that (6÷2) could at one time have been the portion multiplied with the (3)
If it was written (6÷2)(1+2), absolutely that is the correct thing to do (expanding brackets), but not if it’s written 6÷2(1+2). If you mean the latter then I’ve never seen that - links?
leaving us 3(3)
You just did division before brackets, which violates order of operations rules. 6÷2(3)=6÷(2x3)=6÷6=1
The calculator section is actually pretty important, because it shows how there is no consensus. Sharp is especially interesting with respect to your comment because all scientific Sharp calculators say it’s 1. For all the other brands for hardware calculators there are roughly 50:50 with saying 1 and 9.
So I’m not sure if you are suggesting that thousands of experts and hundreds of engineers at Casio, Texas Instruments, HP and Sharp got it wrong and you got it right?
There really is no agreed upon standard even amongst experts.
it shows how there is no consensus
Used to not be. Except for Texas Instruments all the others reverted to doing it correctly now - I have no idea why Texas Instruments persists with doing it wrong. As you noted, Sharp has always done it correctly.
There really is no agreed upon standard even amongst experts
Yes there is. It’s taught in literally every Year 7-8 Maths textbook (but apparently Texas Instruments don’t care about that).
Hi, expert here, calculators have nothing to do with it. There’s an agreed upon “Order of Operations” that we teach to kids, and there’s a mutual agreement that it’s only approximately correct. Calculators have to pick an explicit parsing algorithm, humans don’t have to and so they don’t. I don’t look to a dictionary to tell me what I mean when I speak to another human.
there’s a mutual agreement that it’s only approximately correct.
No there isn’t. I’ve never seen a single Year 7-8 Maths textbook that is in the slightest bit ambiguous about it. The Distributive Law has to literally always be applied (hence why it’s a law). dotnet.social/@SmartmanApps/110819283738912144
The order of operations is not the same as the distributive law.
The first step in order of operations is solve brackets. The first step in solving unexpanded brackets is to expand them. i.e. The Distributive Law. i.e. the ONLY time The Distributive Law ISN’T part of order of operations is when there’s no unexpanded brackets in the expression.
The distributive law has nothing to do with brackets.
The distributive law can be written in PEMDAS as a(b+c) = ab + ac, or PEASMD as ab+c = (ab)+(ac). It has no relation to the notation in which it is expressed, and brackets are purely notational.
The distributive law has nothing to do with brackets
BWAHAHAHA! Ok then, what EXACTLY does it relate to, if not brackets? Note that I’m talking about The Distributive LAW - which is about expanding brackets - not the Distributive PROPERTY.
a(b+c) = ab + ac
a(b+c)=(ab+ac) actually - that’s one of the common mistakes that people are making. You can’t remove brackets unless there’s only 1 term left inside, and ab+ac is 2 terms.
ab+c = (ab)+(ac)
No, never. ab+c is 2 terms with no further simplification possible. From there all that’s left is addition (once you know what ab and c are equal to).
brackets are purely notational
Yep, they’re a grouping symbol. Terms are separated by operators and joined by grouping symbols.
No, those companies aren’t wrong, but they’re not entirely right either. The answer to “6 ÷ 2(1+2)” is 1 on those calculators because that is a badly written equation and you(not literally you, to be clear) should feel bad for writing it, and the calculators can’t handle it with their rigid hardcoded logic. The ones that do give the correct answer of 9 on that equation will get other equations wrong that it shouldn’t be, again because the logic is hardcoded.
That doesn’t change the fact that that equation worked out on paper is absolutely 9 based on modern rules of math. Calculate the parentheses first, you then have 6 ÷ 2(3). We could solve from here, but to make the point extra clear I’m going to actually expand this out to explicit multiplication. “2(3)” is the same as “2 x 3”, so we can rewrite the equation as “6 ÷ 2 x 3”. All operators now inarguably have equal precedence, which means the only factor left in which order to do the operations is left to right, and thus division first. The answer can only be 9.
If you’d ever taken any advanced math, you’d see that the answer is 1 all day. The implicit multiplication is done before the division because anyone taking advanced math would see 2(1+2) as a term that must be resolved first. The answer still lies in the ambiguity of the way the problem is written though. If the author used fractions instead of that stupid division symbol, there would be no ambiguity. It’s either 6/2 x 3 = 9 or [6/(2x3)] = 1. Comment formatting aside, if someone put 6 in the numerator, and then did or did NOT put all the rest in the denominator underneath a horizontal bar, it would be obvious.
TL;DR It’s still a formatting issue, but 9 is definitely not the clear and only answer.
The answer still lies in the ambiguity of the way the problem is written though
But it’s not ambiguous, as per the reason you already gave.
If the author used fractions instead of that stupid division symbol
If you use fractions then the whole thing is a single term, if you use division it’s 2 terms.
9 is definitely not the clear and only answer
1 is definitely the only answer.
"The obelus is treated differently,” Church said. "It could mean ratios, division or numerator and denominator, and these all tweak the meaning of the symbol.”
This is the only symbols I’ve ever seen used (but feel free to provide a reference if you know of any where it isn’t - the article hasn’t provided any references)…
Ratio is only ever colon.
Division is obelus (textbooks/computers) or slash (computers, though if it’s text you can use a Unicode obelus).
Fraction is fraction bar (textbooks) or obelus/slash inside brackets (computers). i.e. (a/b).
those calculators because that is a badly written equation
It’s not badly written, and the reason Texas Instruments gets it wrong is right there in their manual (disobeys The Distributive Law).
modern rules of math
The order of operations rules haven’t changed in at least 100 years, and more likely at least 400 years. Don’t listen to Youtubers who can’t cite a single Maths textbook.
“2(3)” is the same as “2 x 3”
No, it’s the same as (2x3), as per The Distributive Law and Terms.
This is a very nice piece that had so much information I did not know. Toward the top of the article I was wishing for footnotes, references or something that would indicate it was not just your opinion, but as I got further into the piece you provided so many great references. I thought the calculator manuals were particularly accessible and convincing. Thanks for a great read!
you provided so many great references
Except for any actual Maths textbooks. Try this instead.
I’ve seen a calculator interpret 1 ÷ 2π as ½π which was kinda funny
All calculators that are listed in the article as following weak juxtaposition would interpreted it that way.
And they’re all wrong dotnet.social/@SmartmanApps/111164851485070719
An e-calculator I’m guessing? (either that or Texas Instruments) Desmos USED TO interpret that correctly, but then they made a change with automatically turning division into fractions and broke it (because if you’ve specified division then it’s not a fraction) dotnet.social/@SmartmanApps/111164851485070719
I believe it was a app , yes
The order of operations is not part of a holy text that must be blindly followed. If these numbers had units and we knew what quantity we were trying to solve for, there would be no argument whatsoever about what to do. This is a question that never comes up in physics because you can use dimensional analysis to check to see if you did the algebra correctly. Context matters.
The order of operations is not part of a holy text that must be blindly followed
No, it’s in Maths textbooks, and must be… blindly followed. :-)
If these numbers had units
…it wouldn’t matter at all. The order of operations comes from the very definitions of the operators themselves. e.g. 2x3 is shorthand for 2+2+2.
Typo in article:
If you are however willing to except the possibility that you are wrong.
Except should be ‘accept’.
Not trying to be annoying, but I know people will often find that as a reason to disregard academic arguments.
Thank you very much 🫶. No it’s not annoying at all. I’m very grateful not only for the fact that you read the post but also that you took the time to point out issues.
I just fixed it, should be live in a few minutes.
A person not knowing the difference in usage between except and accept sounds like a perfectly reasonable reason to disregard their math skills.
Especially when said person keeps making incorrect statements about Maths and ignores completely what is taught in high school.
academic arguments
The “academic arguments” can be ignored since this is actually high school Maths - it’s taught in Year 7-8.
isn’t that division sign I only saw Americans use written like this (÷) means it’s a fraction? so it’s 6÷2, since the divisor (or what is it called in english, the bottom half of the fraction) isn’t in parenthesis, so it would be foolish to put the whole 2(1+2) down there, there’s no reason for that.
so it’s (6/2)*(1+2) which is 3*3 = 9.
the other way around would be 6÷(2(1+2)) if the whole expression is in the divisor and than that’s 1.
tho I’m not really proficient in math, I have eventually failed it in university, but if I remember my teachers correctly, this should be the way. but again, where I live, we never use the ÷ sign, only in elementary school where we divide on paper. instead we use the fraction form, and with that, these kind of seemingly ambiguous expressions doesn’t exist.
The ÷ sign isn’t used by “Americans”, it’s used by small children. As soon as you learn basic mathematical notation in your introductory algebra class, you’ve outgrown the use of that symbol.
The ÷ sign isn’t used by “Americans”, it’s used by small children
I don’t know where you’re from, but it’s used universally in Australia - textbooks, calculators, all ages - and from what I’ve seen the U.K. too.
Children here in the Netherlands use : as a divisor symbol. I don’t know whether the ÷ sign is particularly American, but it’s not universal.
written like this (÷) means it’s a fraction?
No, that means it’s a division. i.e. a÷b. To indicate it’s a fraction it would need to be written as (a÷b). i.e. make it a single term. Terms are separated by operators and joined by grouping symbols (such as brackets or fraction bars).
put the whole 2(1+2) down there, there’s no reason for that.
There is - it’s a single bracketed term, subject to The Distributive Law. i.e. the B in BEDMAS.
It seems Americans are taught pemdas and not bodas.
I Looked up doing factorials and n! = n(n – 1) is used interchangeably with n! = n*(n – 1)
So Americans will multiply anything first. This is why I put 6 ÷ ( n*(n – 1)) in excel to avoid confusion.
I Looked up doing factorials and n! = n(n – 1) is used interchangeably with n! = n*(n – 1)
Yeah, there’s a problem with some lazy textbook authors, which I talked about here. A term is defined as ab=(axb), and yet many textbooks lazily write it as ab=axb, which is fine if that’s the whole expression, but NOT fine if the expression is a/bc (a/(bxc) and a/bxc AREN’T the same thing!), and so we end up with people removing brackets prematurely and getting wrong answers. In other words, in your case, only n!=n(n – 1) and n!=(nx(n – 1)) can be used interchangeably.
I Looked up doing factorials and n! = n(n – 1) is used interchangeably with n! = n*(n – 1)
yeah, the way I have been taught is that either you put the multiplication sign there or not, it’s the exact same, there’s absolutely no difference in n(n-1) and n*(n-1). in the end, you treat it like the * sign is there and it’s just matter of convenience you can leave it off.
there’s absolutely no difference in n(n-1) and n*(n-1)
There is - the first is 1 term and the 2nd is 2 terms. Makes a difference if it’s preceded by a division.
it’s just matter of convenience you can leave it off.
It’s a matter of how many terms as to whether it’s there or not.
Americans use PEMDAS, in the UK we use BODMAS, and I assume other English speaking countries use one or the other, but there is no difference between them in terms of order of operations, because it’s:
-
brackets (parenthesis)
-
orders (exponentials)
-
division & multiplication (multiplication & division), performed left to right
-
addition & subtraction, performed left to right
People who choose to divide or multiply first because of the acronym have just forgotten that they go together left to right.
-
Interesting, I didn’t know about strong implicit multiplication. So I would have said the result is 9. All along my studies in France, up to my physics courses at University, all my teachers used weak implicit multiplication. Could be it’s the norm in France, or they only use it in math studies at University.
In a scientific context it’s actually very rare to run into that issue because divisions are mostly written as fractions which will completely mitigate the issue.
The strong implicit multiplication will only cause ambiguity after a division with inline notation. Once you use fractions the ambiguity vanishes.
In practice you also rarely see implicit multiplications between numbers but mostly between variables or variables and their coefficients.
Yes of course, we always used fractions so there was no ambiguity. Last time I saw the division symbol must have been in primary school!
You would’ve done dividing by fractions in high school, which requires both. Fractions and division aren’t the same thing.
Def not a math major (BS/PharmD), but your explanation was like seeing through a visual illusion for the first time! lol
I was always taught PEMDAS growing up, and that the MD and the AS was read left to right in an equation like above. But stating the division as a fraction completely changes my mind now about how this calculation works. I think what would happen in a calculation I use every day if the former was used.
Example: Cockcroft-Gault Equation (estimation of renal function)
(140-age)(kg) / 72(SCr) vs (140-age) X kg ➗72 X SCr
In the first eq (correct one) an 80yo patient who weighs 65kg and has an SCr ~ 1.5 = 36.11
In the latter it = 81.25 (waaay too high for an 80yo lol)
edit: calculation variable
But stating the division as a fraction completely changes my mind now about how this calculation works
But division and fraction aren’t the same thing - the former separates terms, the latter is a single term.
(140-age)(kg) / 72(SCr) vs (140-age) X kg ➗72 X SCr
The different answers for these two isn’t because of / vs ➗, but because in the second one you have added extra multiplications in, thus breaking up some of the terms, and SCr has consequently been flipped from being in the denominator to being in the numerator. i.e. AK/72Scr vs. AK/72xSCr.
I didn’t know until now that I unconsciously use strong implicit multiplication (meaning that I get the answer “1”). I believe it happens more or less as a consequence of starting inside the parentheses and then working my way out.
It is a funny little bit of notational ambiguity, so it is funny that people get riled up about it.
It is a funny little bit of notational ambiguity
It’s not ambiguous - it’s The Distributive Law. You got the correct answer, you just forgot what the rule is called (as opposed to people who forget the rule altogether).
My TI-84 Plus is my holy oracle, I will go with whatever it says.
And then get distracted and play some Doom.
TI calcs give the wrong answer, and it’s in their manual why - they only follow the Primary School rule (“inside the brackets”), not the High School rule which supersedes it (The Distributive Law).
It will give 9, just like my 89 emulator. It treats division like a fraction. For a TI, the entire denominator of a fraction needs to be in parentheses or you get into trouble.
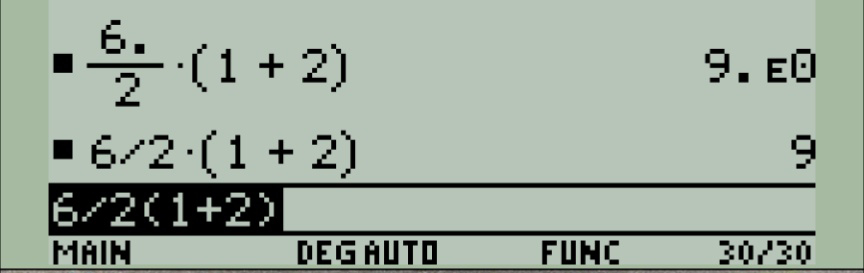
It treats division like a fraction
Which is why it gives the wrong answer.
Also you shouldn’t be adding a dot between the 2 and the brackets - that also changes the answer.
I found a few typos. In the 2nd paragraph under the section “strong feelings”, you use “than” when it should be “then”. More importantly, when talking about distributive properties, you say x(x+z)=xy+xz. I believe you meant x(y+z)=xy+xz.
Otherwise, I enjoyed that read. I’m embarrassed to say that I did think pemdas meant multiplication came before division, however I’m proud to say that I’ve unconsciously known that it’s important to avoid the ambiguity by putting parentheses everywhere for example when I make formulas in spreadsheets. Which by the way, spreadsheets generally allow multiplication by juxtaposition.
I believe you meant x(y+z)=xy+xz.
Actually it should be x(y+z)=(xy+xz), as that’s exactly where a lot of people go wrong. They go from 6/2(1+2) to 6/2x3, instead of to 6/(2x3), and thus end up with the wrong answer (cos that flipped the 3 from being in the denominator to being in the numerator. i.e. instead of dividing by 3 they are now multiplying by 3, all because they removed brackets prematurely).
Thank you so much for taking the time and reading the post. I just fixed the typos, many thanks for pointing them out.
There is nothing really to be embarrassed about and if you look at the comment sections of such viral math posts you can see that you are certainly not the only one. I think that mnemonics that use “MD” and “AS” without grouping like in “PE(MD)(AS)” are really to blame here.
An alternative would be to drop the inverse and only use say multiplication and addition as I suggested with “PEMA” but with “PEMDAS” one basically sets up students for the problem that they think that multiplication comes before division.
I am so glad that nothing I do in life will ever cause this problem to matter to me.
The way I was taught in school, the answer is clearly 1, but I did read the blog post and I understand why that’s actually ambiguous.
Fortunately, I don’t have to care, so will sleep well knowing the answer is 1, and that I’m as correct as anyone else. :-p
why that’s actually ambiguous.
It isn’t actually ambiguous. You have remembered what you were taught in school, unlike the author of the blog post, who manages to write the whole thing without ever once checking a Maths textbook (which would reveal the only correct answer to be 1).
What if the real answer is the friends we made along the way?
That’d be good, but what I’ve found so far here is a whole bunch of people who don’t like being told the actual facts of the matter! 😂
I think this speaks to why I have a total of 5 years of college and no degree.
Starting at about 7th grade, math class is taught to every single American school child as if they’re going to grow up to become mathematicians. Formal definitions, proofs, long sets of rules for how you manipulate squiggles to become other squiggles that you’re supposed to obey because that’s what the book says.
Early my 7th grade year, my teacher wrote a long string of numbers and operators on the board, something like 6 + 4 - 7 * 8 + 3 / 9. Then told us to work this problem and then say what we came up with. This divided us into two groups: Those who hadn’t learned Order of Operations on our own time who did (six plus four is ten, minus seven is three, times eight is 24, plus three is 27, divided by nine is three) Three, and who were then told we were wrong and stupid, and those who somehow had, who did (seven times eight is 56, three divided by nine is some tiny fraction…) got a very different number, and were told they were right. Terrible method of teaching, because it alienates the students who need to do the learning right off the bat. And this basically set the tone until I dropped out of college for the second time.
Yes, unfortunately there are some bad teachers around. I vividly remember the one I had in Year 10, who literally didn’t care if we did well or not. I got sick for an extended period that year, and got a tutor - my Maths improved when I had the tutor (someone who actually helped me to learn the material)!
A fair criticism. Though I think the hating on PEDMAS (or BODMAS as I was taught) is pretty harsh, as it very much does represent parts of the standard of reading mathematical notation when taught correctly. At least I personally was taught its true form was a vertical format:
B
O
DM
AS
I’d also say it’s problematic to rely on calculators to implement or demonstrate standards, they do have their own issues.
But overall, hey, it’s cool. The world needs more passionate criticisms of ambiguous communication turning into a massive interpration A vs interpretation B argument rather than admitting “maybe it’s just ambiguous”.
The problem with BODMAS is that everybody is taught to remember “BODMAS” instead of “BO-DM-AS” or “BO(DM)(AS)”. If you can’t remember the order of operations by heart you won’t remember that “DM” and “AS” are the same priority, that’s why I suggested dropping “division” and “subtraction” entirely from the mnemonic.
It’s true that calculators also don’t dictate a standard but they implement what conventions are typically used in practice. If a convention would be so dominating (let’s say 95% vs 5%) all calculator manufacturers would just follow the 95% convention, except maybe for some very special-purpose calculators.













