Yea that’s not explained better than a math teach. They just swapped notation common in math, for notation common in one specific programming language. it’s only easier for the audience who happens to be familiar with programming in general, and that language in particular.
one specific programming language
I think you’d be hard pressed to find someone with any sort of programming background, even just as a hobbyist, who doesn’t understand that for loop notation, whether or not they know the specific language it’s from. (I couldn’t even tell you what specific language that’s from, because that notation matches so many different ones.)
I have a 15 year old son; he definitely has not seen summation in math classes yet, but he has far more than enough programming experience (even just from school) to understand the for loop.
I think its Java.
Java/C# would have types before the variables:
double sum = 0d; for (int i = 0; i < 4; i++) sum += 3 * i;Only if they’re declared in the snippet.
It’s any C derivative language.
Could also be Javascript or C#.
Or C or C++
I think the concept of a for loop is easier to learn, even for non-programmers, as biased as I may be.
Fuck! Im 40 and this is the first time I understand the sigma sign!! Thank you!
Couldnt they just show this to me at 7th grade or something when i already learned pascal?
I was into coding (javascript) but nope they are unwilling to find creative new ways to help teach people, gotta be a nonseical “one size fits all”
The sigma sign shows up as “sum” quite a bit but I didn’t know about the for-loop thing.
Wouldn’t reducer be more precise?
Definitely, although I’m sure that under the hood it’s all the same. Some (albeit high-level) languages also support a sum function that takes a generator as an input, which seems pretty close to this math notation.
I think this is pretty much the imperative equivalent of
foldl (\acc i -> acc + 3*i) 0 [1..4].Can you explain this out a bit more? I’m a self-taught programmer, of sorts, and I’m not quite getting this…
A reducer “reduces” a list of values to one value with some function by applying it to 2 values at the time.
For instance if you reduce the list [1, 2, 3] with the sum function you get (1 + (2 + 3)) = 6.
I remember how confused I was when I first encountered i=i+1… like, what 🤨? How can this be correct, this thing has to be wrong… and then you start seing the logic behind it and you’re like “oooh, yeah, that seems to work… but still, this is wrong on almost every level in math”… and then you grow a bit older and realize that coding has nothing to do with math, instead it’s got everything to do with problem solving. If you like to name your variables peach, grape, c*nt, you can, and if that helps you solve the problem, even better, just make it work, i.e. solve the problem 🤷.
coding has nothing to do with math
A monad is just a monoid in the category of endofunctors, what’s the problem?
I’m not that good of a coder or mathematitian to know what that quote means 😂😀.
It’s from a longer quote in “A Brief, Incomplete and Mostly Wrong History of Programming Languages” about the language Haskell:
1990 - A committee formed by Simon Peyton-Jones, Paul Hudak, Philip Wadler, Ashton Kutcher, and People for the Ethical Treatment of Animals creates Haskell, a pure, non-strict, functional language. Haskell gets some resistance due to the complexity of using monads to control side effects. Wadler tries to appease critics by explaining that “a monad is a monoid in the category of endofunctors, what’s the problem?”
Some other languages like e.g. Rust also use monads. The point I was trying to make humorously was that many programming languages sometimes do use math concepts, sometimes even very abstract maths (like monads), and while it’s not maths per se, programming and computer science in general can have quite a bit to do with maths sometimes.
Yeah, I get what you’re trying to say now 😉. Still, they’re mostly used when doing algos, which in real world practical examples is almost never. We do all sorts of repetitive things, like sorting or user input blocks, but new algos is… something that you might do in NASA, CERN, Wall Street, not your every day programming job. Sure, you might optimize a thing or two here and there, but that’s about it 🤷.
Coding has nothing to do with math yet the entire basis of computing and programming is Boolean algebra.
I meant as in real world applications, like how much math do you need to know to sort a table or search through an array.
But isn:t that kinda true for most things? If you go down deep enough, amost all tasks end up in physics und thus maths somewhere. But if I’m stacking shelves, I don’t care that there are some pretty complicated mathy physics things that determine how much weight I can stack on the shelf. I just stack it.
That’s kinda how most of programming is related to maths. Yeah, math makes it all run, but I mostly just see maybe a little algebra and very simple boolean logic.
And the rest of my work is following best practices and trying to make sense of requirements.
you don’t need to worry about the load capacity of the shelf, but only because somebody else already engineered it to be sufficient for the expected load. i’d argue that you aren’t the coder in this analogy, you’re the end user.
But how often, as a coder, are you going low-level?
If I want to sort a list, I don’t invent a sorting algo.
I don’t even code out a known sorting algo.
I just type
.sort(), and I don’t even care which algo is used.Same with most other things. Thinking about different kinds of lists/maps/sets is something you do in university.
In reality, many languages (like e.g. Python) don’t even give you the choice. There are
List(), Map(), Set()and that’s it. And even on languages like Java, everybody just goes for ArrayList, HashMap and HashSet. Can’t remember a single time since university where I was like “You know what I’d fancy now? A LinkedList.”I honestly don’t even know if Java offers any Map/Set implementations that don’t use hash buckets.
And even of boolean logic we only use a fraction. We use and, or, not and equals. We don’t use nand, nor, identity, xor, both material conditional variants, material biconditional or their negations.
This is what I was actually trying to say, thanks for elaborating 👍.
and then you grow a bit older and realize that coding has nothing to do with math, instead it’s got everything to do with problem solving.
Wait until you realize what math is all about
I think I do understand, but I’d rather embarres myself 😂.
I mean, coding does have to do with math, it’s usually just different notation. i = i + 1 in math notation is just i := i + 1.
That’s advanced calculus, and my guess is, those notations were made up to give rise to a new field in math, which has more to do with computers than math, so I don’t think that counts.
What discipline do you think Allan Turing and Von Neumann were in?
Computation theory, but that’s not math as in regular math. It’s just a fancy way of expressing how things inside a computer work, so we can actually make better versions of it. You just have to express it somehow in math terms.
It’s like saying engineers use math all the time. No, they don’t. We use simple aproximations of what is actually happening to dumb down the problem, cuz, it does the job nicely and no one will notice the difference between what we used, a simple aproximation, and the real thing, a full blown advanced calculus model of the thing we’re working on.
You mean they were not mathematics department professors?
Where?
The biggest difference (other than the existence of infinity) is that the upper limit is inclusive in summation notation and exclusive in for loops. Threw me for a loop (hah) for a while.
i thought this was pretty weird too when i found out about it. i’m not entirely sure why it’s done this way but i think it has to do with conventions on where to start indexing. most programming languages start their indexing at 0 while much of the time in math the indexing starts at 1, so i=0 to n-1 becomes i=1 to n.
My abstract math professor showed us that sometimes it’s useful to count natural numbers from 1 instead of 0, like in one problem we did concerning the relation Q on A = N × N defined by (m,n)Q(p,q) iff m/n = p/q. I don’t hate counting natural numbers from 1 anymore because of how commonly this sort of thing comes up in non-computer math contexts.
yeah thats a good example and it shows weird the number 0 is compared to the positive integers. it seems like a lot of the time things are first “defined” for the positive integers and then afterwards the definition is extended to 0 in a “consistent way”. for example, the idea of taking exponents an makes sense when n is a positive integer, but its not immediately clear how to define a0. so, we do some digging and see that am+n = aman when m and n are positive integers. this observation makes defining a0=1 “consistent” with the definition on positive integers, since it makes am+n = aman true when n=0.
i think this sort of thing makes mathematicians think of 0 as a weird index and its why they tend to prefer starting at 1, and then making 0 the index for the “weird” term when it’s included (like the displacement vector in affine space or the constant term in a taylor series).
Nah, look at the implementation above:
n <= 4Means it’s inclusive.
You’re probably referring to some other implementation that doesn’t involve such fine control, like Python where
range(4)means[]Oh yeah, I meant generally. Isn’t it most common if not best practice to say
for (i = 0; i < whatever; i++)?Fair. I guess to accommodate zero-indexing so that it still happens
whatevertimes, notwhatever + 1times.
real
You can reduce this readable code into one line of confusing python list comprehension that runs 100x slower!
I don’t think you can use python list comprehensions in this case, since you don’t want a new list, but rather reduce it to a single value.
Yes, the classic readability of c style for loops.
How about some Haskell
let numbers = [1, 2, 3, 4, 5] let sumOfNumbers = sum numbers
What’s wrong with list comprehensions? Do I just have Stockholm Syndrome at this point?
I would skip the square brackets and just use a generator expression:
sum(3*n for n in range(5)).
Removed by mod
Which makes the integral sign ∫ a non-discrete for-loop
That does not help. What does non-discrete mean?
Continuous.
Instead of jumping from 1 to 2 to 3, we move smoothly across all (typically real) numbers. Obviously this would go to infinity almost every time because there are infinite real numbers between any two distinct real numbers. So instead, we merge it into a bunch of skinny rectangles with their bottom on the x axis and the top at the value of the function for the start of the rectangle. As we shrink the width of the rectangles, it approaches the continuous notion.
Continuous means “smooth” - there are no jumps Discrete means there are jump
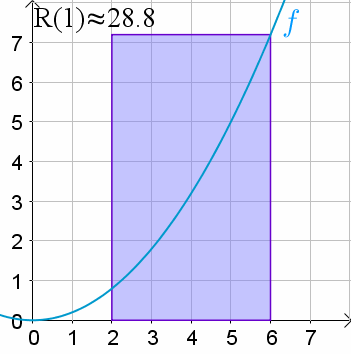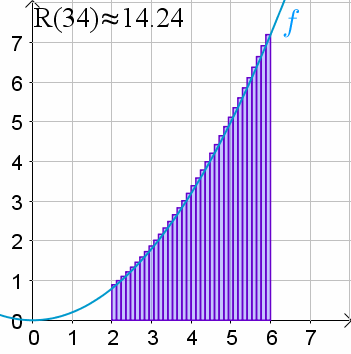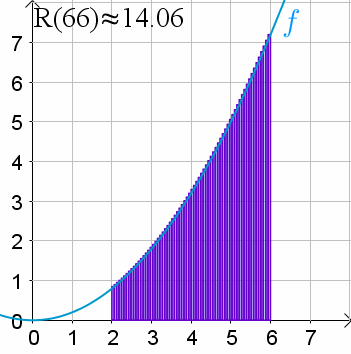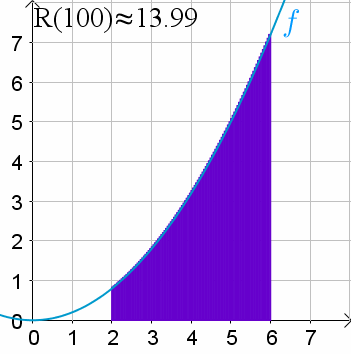
Short answer: Imagine that the integer used in the for loop is a float instead.
Longer, a bit more precise answer: An integer can only have discrete values (i.e. -1, 0, 1, 2, …, 69, … etc.)
A real number (~float with infinite precision) can have an infinite amount of values between two discrete values.
An integral is, to put it simpy, a sum of all the results of taking those infinite values between two discrete values (an interval) and feeding them to the given function.
It’s a for loop over an infinite set of real numbers rather than over a finite set of integers => a non-discrete for loop
if you take a modular approach and allow different measures to be used, it also lets the integral sign be a discrete for-loop
test
Maybe I’m crazy but they did teach me this in school. “This means so this operation until conditions are met”.
I disagree. It’s a while loop, because a for-loop is finite, so you can’t count to infinity with it.
I wanna see how you get a while loop to actually go to infinity. I’ll wait…
on second thought, no I won’t.
for (i=0; true; i++)there is no reason for a (non-foreach) for loop to be any more or less finite than a while loop.
for (a; b; c) { d; }is just syntactic sugar for
{ a; while (b) { d; c; } }in most or all languages with c-like syntax.
There’s nothing special about a generic for loop (at least in C-like languages). There’s no reason you couldn’t do something like
for (i = 0; true; i++)to make it infinite. Some languages even support an infinite list generator syntax likefor i in [0..](e.g. it lazily generates 0, then 1, then 2, etc. on each iteration) so you can use a for-each style loop to iterate infinitely.Now, whether or not you should do such things is another question entirely. I won’t pretend there aren’t any instances where it’s useful, but most of the time you’re better off with a different structure.
The education system creates scarcity of knowledge to increase the profit of investment and spending, everything complex can be broken down into simple forms.
Sounds as a conspiracy theory
Everything dealing with capitalism ends up sounding like a conspiracy theory. You’re like “of course people wouldn’t actually take this thing we, as humans, need and sell it,” when suddenly air has been commodified and those who can’t afford it are dlseen as not deserving of air.
He’s missing the sigh() function call at the start of the main body of the loop.
When you study CompSci (depending on where IG) you tend to see them that way when trying to mathematically prove something about an algorithm. It’s only really a good way of thinking if you’re into coding, but I don’t think a teacher for a non-coding related algebra class should show this, it can be really confusing for some people.
I liked this so much I tried to find more. A few seconds googling turned up a lot, but this is the first hit: https://amitness.com/2019/08/math-for-programmers/
Hi, you can look into “discrete mathematics” if you’re interested in the overall subject of math for programmers, it was one of my hardest class but highly intesting!
That sounds perfect because I don’t want anyone to know I’m studying math.
I was “good at math” in school and all through uni. Discrete mathematics crushed me.
Dude, 🔥👍













